|

|
|||
La simulation d'écoulements complexes multimatériaux est devenue, en quelques années, un enjeu stratégique pour de nombreuses entreprises et entités de recherche. Elle est désormais un outil indispensable en amont de la phase de réalisation d'un projet (afin de limiter le nombre de prototype, diminuer le coût des essais, simuler des conditions de plus en plus drastiques, accélérer la mise sur le marché des produits en améliorant sans cesse la qualité…), que l'on retrouve dans divers domaines tels que les transports, la défense, l'aéronautique, la météorologie. Il existe trois classes de schémas numériques aujourd'hui utilisés pour résoudre des problèmes industriels :
Les schémas ALE les plus répandus sont les schémas Lagrange + Projection, qui consistent à utiliser un schéma Lagrangien pour calculer la solution numérique, et à régulariser la solution dès que la déformation du maillage devient trop forte. Cette régularisation consiste simplement à interpoler (à « projeter ») la solution numérique du maillage déformé sur un maillage beaucoup plus régulier. On parle alors d'ALE indirect, car le schéma est défini en deux étapes : une étape lagrangienne, suivie d'une étape de projection. La Direction d'Ile de France (DIF) du Commissariat à l'Energie Atomique collabore depuis plusieurs années avec Eurobios pour développer une classe de schémas ALE directs qui pourraient s'intégrer rapidement dans leurs codes de production. Il s'agissait d'une part de développer un schéma multidimensionnel qui gère plusieurs types de matériaux, et d'autre part un module qui permet un contrôle du maillage en fonction de l'écoulement.
.
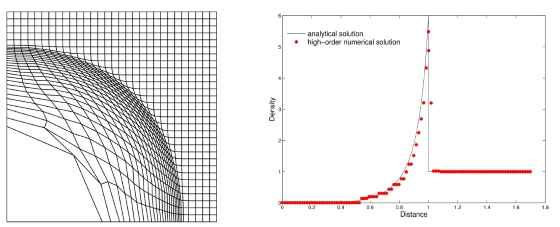
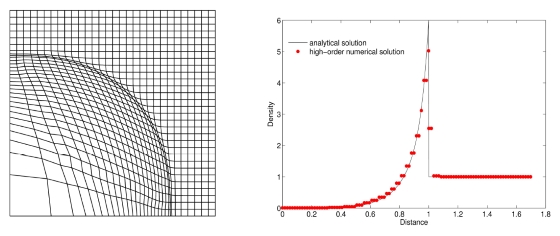
. Figure 1: Validation du schéma par le cas test de la détonation de Sedov. En haut, simulation Lagrangienne. En bas simulation ALE. La densité est donnée par les courbes représentées en points rouge Sur la figure 1, les résultats de simulation du cas test de la détonation de Sedov sont représentés. Ce cas test consiste à simuler la propagation d'une onde de détonation issue de l'injection rapide d'énergie dans la maille du coin inférieur gauche du domaine de calcul. Ce cas ne présente pas de déformation critique, mais le déplacement du maillage dans le cas Lagrangien conduit à une expansion démesurée de la maille de coin (grosse maille sur le maillage du haut), induisant une perte de précision de calcul dans cette maille. Pour le schéma ALE, le maillage reste régulier tout au long de la simulation. Les profils de densité (à droite) prouvent que la solution numérique ALE reproduit fidèlement la solution analytique, montrant un gain de précision dans la région de détente par rapport au schéma Lagrangien. Actuellement, les études en cours s'appuient à étendre ce schéma pour des simulations multimatériaux.
|
|